陽電子消滅法による複合材料の機械・物理特性評価への応用
FRP学術業界動向としてPositron annihilation spectroscopy、日本語だと陽電子消滅法と呼ばれる分析手法を用いた、複合材料の機械・物理特性評価への応用について概要を述べたいと思います。
陽電子とは
陽電子は電子の反粒子です。
陽電子と電子は同じ静止質量とスピンを有しますが、
電荷が正、つまり電子と逆です。
一昔前に流行った「天使と悪魔」という小説でも反物質が登場し、
それがヴァチカン爆破テロに使われるという計画が述べられています。
「無」から突然原子や分子、さらに細かいことを言えば素粒子が生まれたわけではなく、
そもそもは物質と反物質が同量存在し、そのうち反物質だけがなぜか消滅し、
物質だけが残ったという”相対性の破れ”について聞いたことがある方もいるかもしれません。
宇宙空間では不安定原子核のβ+崩壊やガンマ線の対生成によって大量に存在する一方、
地球上だと陽電子は電子と極めて短い時間で対消滅してしまいます。
カール・デイヴィッド・アンダーソンという物理学者は、
この陽電子の発見の貢献によるノーベル物理学賞を授与されています。
陽電子消滅法：Positron annihilation spectroscopyの概要
陽電子消滅法については、私も所属する応用物理学会の学会誌に掲載されていた、
以下の解説記事を参考にしました。
※参考情報
上殿 明良. 陽電子消滅を用いた材料評価. 応用物理, 2025, 94, 9, p.478.
陽電子消滅法は非破壊による分析手法の一つで、
陽電子が物質中の電子と対消滅するという前述の特性を応用しています。
Na-22やCo-58といった放射性同位体から陽電子を発生させ、
それを1eV以下のエネルギーまで落とした後に電場で再加速させて物質に照射し、
その結果生じるγ線や陽電子密度分布を評価します。
照射された陽電子の挙動と内部欠陥による影響
物質に照射された陽電子は熱化過程と呼ばれるエネルギー損失の工程を経て、
存在する電子と対消滅します。
この対消滅の発生と同時に2本のγ線が放出され、
それぞれのエネルギー値は511keVであることが分かっているとのこと。
ここで仮に物質内に空隙などの内部欠陥がある場合、
イオン核から受けるクーロン反発力と呼ばれるものの影響により、
陽電子は”捕獲”されて消滅するという性質があるようです。
格子空間が大きいと陽電子寿命が延びる
前出の参考情報では密度汎関数理論に基づくシミュレーションから、
規則的な原子配列がある場合と格子欠陥がある場合で、
照射された陽電子の密度分布に違いがでることを示しています。
この理由は格子欠陥の様な他と比べて広い空間では、
陽電子の寿命が”延びる”ことが原因とのこと。
つまり欠陥のようなものが多いほうが、陽電子が長く存在するという性質を応用し、
内部欠陥有無の評価に応用しています。
ただその違いは0.1ns（nはナノ）レベルですので、100億分の1秒レベルと極めて短い時間です。
陽電子消滅法の主たる評価手法
陽電子消滅法と一言で言っても複数の評価手法があるようです。
前述の陽電子の消滅までの時間を測定するのが陽電子寿命測定で、
Positron Annihilation Lifetime Spectroscopy（PALS）と呼ばれます。
原理は既に述べた通りです。PALSを用いた複合材料の評価に関する学術論文をこの後ご紹介します。
それ以外には対消滅の際に発生するガンマ線のエネルギーの広がりを分析するDoppler Broadening （DB）Spectroscopy、当該2本のガンマ線の角度ずれを評価するAngular Correlation of Annihilation Radiationがあるようです。
前者はSパラメータ（低運動量成分、空孔関連）とWパラメータ（高運動量成分、核心電子関連）を用い、欠陥の化学環境を評価するとのこと。
空隙の大きさ反比例してγ線のエネルギー分布が小さくなることからそのサイズを同定するイメージのようで、この広がり変化をS（Shape）とW（Wing）で示すようです。
このパラメータも後述する学術論文で出てきます。
この辺りのイメージは、既述の参考情報と同じ執筆者の先生が以下の記事で分かりやすく解説されています。
※参考情報
上殿 明良. 陽電子消滅を用いた材料評価. 応用物理, 2010, 79, 4, p.307.
Angular Correlation of Annihilation Radiationは結晶構造の評価などに用いられるようです。
次に陽電子消滅法を用いた複合材料の評価に関する学術論文をご紹介します。
陽電子消滅法を用いた複合材料評価に関する学術論文
ご紹介するのは以下の学術論文です。
上記の学術論文は有償ですが、Academia.eduの会員の方は無料で読むことができます。
私も当該サイト経由で論文を入手しました。
概要を以下に述べます。
PALSの結果と複合材の材料特性の相関を評価するのが目的
本論文の主目的は既述のPALSの評価結果と、
その評価対象の複合材料の機械・物理特性の関係性を見ることにあります。
エポキシ樹脂にアルミナ、酸化ケイ素、炭素の微細粉末を添加した複合材が評価対象
評価対象となっている複合材料は、
エポキシ樹脂（Araldite LY 1092 / the adequate hardener HY1092）に、
アルミナ、酸化ケイ素、炭素（カーボン）をそれぞれ0.5、1.5、3.0 wt%添加したものになります。
添加後は超音波で混合しているようです。
評価項目は硬度、引張強度/弾性率
材料特性として評価しているのは硬度と引張強度/弾性率です。
硬度はRockwell A、引張特性はDIN 53457で評価しているとのこと。
引張試験の試験片サイズは150 X 15 X 3 mm（L/W/T）で、試験速度2 mm/minで評価しています。
弾性率の予想には複合則に加えPaul modelを検討
引張弾性率の予想にはFRPでもよく使われる複合則に加え、
Paul modelでの評価も行っています。
Paul modelは強化材（ここでいう微粉末）の弾性率をマトリックス樹脂の弾性率で割ったm、
並びに強化材の体積分率Vp、そしてマトリックス樹脂の引張弾性率Emを用いて、
複合材料の引張弾性率Ecを下式で予想します。論文中の式(1)で示されています。
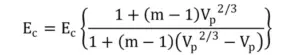
結果によると複合則よりもこのPaul modelの方が引張弾性率を、
より的確に予想できたとのことです。
これ以外にもCounto modelというものについても触れられています。
詳細は論文中の式(3)をご参照ください。
用いた陽電子消滅法の概要
PALSが基本で、陽電子発生源はNa-22です。
測定はすべて室温、大気中で行われ、
一測定あたり100万データ以上の測定データの積算によって陽電子寿命のスペクトルを取得しているとのこと。
ある程度ばらつきもあるようで、FIT値と呼ばれる数値で1.04から1.2の間にあるものを、
実際の結果として採用しているようです。
陽電子寿命長さで3つに分類
寿命長さは短いもの、中間程度のもの、長いものの3成分に分類し、
それぞれτ1、τ2、τ3と定義することが述べられています。
既述の通り陽電子の寿命が長いほうが大きな欠陥があると解釈できます。
さらにそれぞれの強度をI1、I2、I3とすると書かれています。
自由体積空隙は分子鎖の隙間の大きさ
樹脂（高分子）にPALSを適用すると自由体積に該当する数値を観測することができるとのことです。
高分子の世界で自由体積を重点的に語ることはあまりないと記憶していますが、
高分子溶液の混合エントロピーの議論に用いるFlory-Hugginsの理論が関係するようです。
当該理論において自由体積とは、
「分子が自由に動くことができる分子間のすきま」
と書かれています。
非晶性高分子に照射された陽電子の一部はポジトロニウム（Ps）という、
電子と陽電子が電磁気力で結合した複合粒子を生成するとのこと。
Psのうちスピンが反平行（一重項）のものをパラポジトロニウム（p-Ps）、
スピン平行（三重項）のものをオルトポジトロニウム（o-Ps）というようです。
このうちo-Psが自由体積空間にトラップされると寿命が延びるという特性を活かし、
自由体積の測定を行うことができるとの理解です。
この辺りについては、以下の参考情報もご参照ください。
※参考情報
萩原英昭. 陽電子消滅寿命測定による高分子材料の自由体積空隙サイズ解析. ぶんせき, 2021, 3, p.93.
今回参照した論文でも自由体積、並びにそこから算出する空孔体積（詳細後述）を評価指標として用いています。
次に結果の要点を抜粋して述べます。
機械/物理特性の結果概要
複合材料の機械/物理特性の結果について述べます。
硬度について
硬度は論文中のFig.1に示されています。
アルミナは添加量に応じて硬度の増加がみられる一方、
カーボンは横ばい、酸化ケイ素は最小添加量最小の0.5wt%の時最大で、
1 wt%以上では低下しています。
低下した場合の理由として、硬化不良の可能性が述べられています。
個人的には凝集の可能性に加え、
そもそも測定のばらつきが大きいことを疑っています。
硬度測定そのものが局所評価である影響も大きいでしょう。
なお、硬化不良を疑うのであれば樹脂をDSCなどで計測し、
硬化に伴う発熱反応ピークから算出できる硬化度で比較すれば明確にできるでしょう。
引張強度/引張弾性率
引張強度
引張強度の結果は論文中のFig.2に示されています。
酸化ケイ素、並びにアルミナを最小添加量である0.5wt%の場合のみ、
引張強度が向上していることが示されています。
一方でそれ以上加えても特性は無添加と変わらず、
さらにカーボンは添加による引張強度向上効果は認められません。
強度低下の理由は微細粉体の凝集にあると書かれています。
私も同意見です。
より具体的には凝集することによって破壊の起点が出現する結果、
低ひずみ領域での応力集中により脆性のエポキシだと亀裂進展しやすい、
という一連の破壊現象によって引張強度は低下したものと考えます。
引張弾性率
論文中のFig.4に結果が示されています。
黒丸で示されるのが実験値です。
これを見ると添加量に応じて基本的には引張弾性率は高まっていることが分かります。
よって、微粒子添加は弾性率向上には効果が出やすいといえます。
私の経験則的にも概ねあっています。
ただし、論文中でも述べられている通り、
弾性率を算出するのは微小ひずみ領域です。
微小領域だからこそ凝集の影響も少なかったといえます。
実際のアプリケーションではそのような微小ひずみ領域だけで使う想定は現実的ではなく、
弾性率だけでなく破断伸びや破断強度が重要視されることもあるでしょう。
また、なぜ弾性率が高まったのに硬度はそうならなかったかについては、
前者は試験片全体のマクロ評価、前出の通り硬度は局所、つまりマクロ評価であることによると考えます。
微細粉末をマトリックス樹脂に添加した複合材料の弾性率はPaul modelによる予測が妥当
Fig.4を見ると黒丸の実験値に対して最も近い近似値を与えているのが、
赤の四角で示されるPaul modelであることが分かります。
FRPで一般的な複合則は特にカーボンとアルミナで予測値が実測値を上回る傾向にあり、
適用に課題があるとの言及があります。
個人的には酸化ケイ素を強化材にした場合の複合材料でやや誤差が大きい結果ですが、
Counto modelも妥当なモデルではないかと感じます。
PALSとDBの結果概要
PALSとDBの結果についてそれぞれ概要を述べます。
PALSの結果について
Fig.7には結晶領域と非晶領域の界面の検知を目的とした、
τ2とI2と微小粉末添加量の関係が示されています。
これを見るとアルミナは3wt%添加するとτ2が増加する、
つまり結晶領域と非晶領域の界面が増加していることから、
樹脂と微細粉末の間の相互作用が生じていることを示唆しているようです。
このことからアルミナはPALSの結果だけを見ると、
1.5wt%添加の時にエポキシ樹脂との相互作用が生じやすい、
つまり複合材料としての性能が発現しやすい状態であると解釈できると考えます。
同様の傾向は酸化ケイ素で認められ、
こちらは0.5wt%より多い添加量でτ2が高まっていることから、
当該材料の微細粉末の添加量は1.0wt%以上の添加によって、
複合材料としての性能が発現しやすい可能性があることが示されています。
カーボンは添加量によらずτ2が高く、
同じ有機物ということもあって複合材料として、
強化材とマトリックス樹脂間で相互作用が生じやすいことがわかります。
ただ引張強度の結果を見るとカーボンは添加効果が認められにくかったことから、
強化材とエポキシ樹脂間の相互作用だけでなく、
τ2の増加は微細粉末の凝集による空隙の発生も示しているのではいかと私は考えます。
自由体積の評価であるτ3とI3
PALSの本命評価の一つである自由体積に関する内容です。
結果は論文中のFig.8に示されています。
τ3を見ると、酸化ケイ素は0.5wt%添加の時に未添加よりも低く、
言ってしまえば空隙などの存在が減少していることが示唆されています。
I3も同時に減少していることがこの考察の妥当性を支持しています。
一方で酸化ケイ素に加え、アルミナも1.5wt%以上添加した場合はτ3が増加傾向であり、
I3も上昇していることから当該添加量以上だと凝集等により空隙が発生している可能性があります。
よくわからないのはカーボンの場合で、τ3は濃度に寄らず概ね高い数値で空隙が示唆される一方、
3wt%添加の場合はI3が大きく低下しています。
この理由は自分ではわからないため、
PALS評価の専門家の方の意見をうかがいたいところです。
論文中では明確な考察の記述は有りませんでした。
自由体積の数値から自由体積の半径である空孔体積（Volume hole）を導入
詳細は論文中の式(4)から(6)に記載があります。
通常自由体積を主に内部欠陥を議論するようですが、
ここでは自由体積を球体形状とみなして、空孔体積（Volume hole）の指標を導入し、
材料特性との比較を行っています。
τ3と体積孔径R、経験則による電子層厚み1.66A（オングストローム）を空孔径に加算したR0を用いると、以下のような経験式が成立するとのことです。
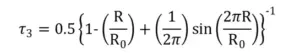
この式によって、τ3が分かれば空孔径がわかり、結果的に空孔体積が分かるという流れです。
また、自由体積（Fv）と空孔体積（Vf）、そしてI3の間には以下のような経験則による関係式があるとのこと（ここでいうVfは単位体積繊維含有率のことではありません）。
Fv=C*Vf*I3
Cは構造に由来する定数のようです。
このCを含む、自由体積と空孔体積の関係式の詳細については、
参照元である以下の論文を読むと詳細が書かれているかもしれません。
※参考情報
Y.C. Jean. Positron annihilation spectroscopy for chemical analysis: A novel probe for microstructural analysis of polymers.
Microchemical Journal, 1990, 42, 1, p.72
https://www.sciencedirect.com/science/article/abs/pii/0026265X90900273
空孔体積と引張強度の間には負の相関を確認
これはFig.12を見ていただくとわかりやすいと思います。
横軸が微細粉末の添加量、縦軸は左が引張強度、右が空孔体積です。
赤線で示される空孔体積が大きいと、
黒線で示す引張強度が低くなっています。
つまり、τ3とI3から得られる空孔体積を評価パラメータとすることが、
複合材料としての特性値の予測に活用できる可能性を示しています。
空孔体積と硬度も基本は負の相関があるが異なる結果も
Fig.15には空孔体積と硬度の関係が示されています。
ただし、引張強度の場合と比較し、負の相関が必ずしも維持されていないことが分かります。
既に述べた通り、硬度は局所的な評価であることがその主因と考えます。
DBの結果について
論文中のFig.9と10に結果が示されています。
横軸が微細粉末の添加量、縦軸がS、Wの各パラメータの値です。
既述の通り、Sパラメータは空孔関連と書かれていることから、
この数値が小さいほうが大きな空隙が生じている可能性が高いと解釈できるものと考えます。
私の理解が正しいかわかりませんが、結果を見るとWパラメータはそれと逆の傾向を示すようです。
これを見ると酸化ケイ素、アルミナ共に1.5wt%添加時にSパラメータは最大値を示し、
空隙が生じやすい状態にあると推測されます。
それに対してカーボンは常に右肩上がりで、
添加しただけ空隙が生じやすいということを示唆しています。
縦軸のパラメータ数値をそのまま比較していいかはよくわかりませんが、
もしそれが可能だとするとアルミナは縦軸のSパラメータの数値が小さく、
上下は入れ替わるものの酸化ケイ素とカーボンが同じ程度です。
もしかすると今回の評価系では、
アルミナが最も欠陥ができにくく、
マトリックス樹脂と強化材が一体化しやすい、
という解釈ができるのかもしれません。
どれもSパラメータと比較し、Wパラメータは逆の傾向を示しています。
このようにSパラメータとWパラメータが負の相関を有する場合、
欠陥の形態が一種類であることを示唆しているとのことです。
次に、今回の結果から考えるべきことについて述べたいと思います。
自由体積よりも空孔体積の方がFRPを含む複合材料評価には活用しやすい
陽電子消滅法というと自由体積を基本に評価するのが多いようですが、
複合材料の評価にあたっては今回の論文で述べられた通り、
空孔体積を軸とした方が活用しやすい可能性が示されたと考えています。
検知できる欠陥精度も極めて高いことから、
超高精度の欠陥検出が望まれるような、
複合材料でいえば脆性材料であるCMCなどには活用できる部分があるかもしれません。
この場合の活用法というのは、量産される製品の検査に用いるというより、
開発段階で亀裂先端の寸法などを高精度で測定し、
亀裂進展有無の観点から欠陥の設計許容値を決めることへの活用が考えられます。
※関連コラム
GE aviation が CMC 向け SiC 製造工場設立
評価できるのは表層から数μmと微小深さ領域である限界を認識する
これは陽電子というそもそも寿命が少ない素粒子を用い、
しかも存在をナノ秒という微小時間で評価するものであり、
数mm以上の厚みが一般的なFRPを想定した場合、
内部状態を見ることは難しいという判断になります。
陽電子消滅法に関する本限界は予め理解する必要があるでしょう。
強化繊維とマトリックス樹脂が存在するFRPでは結果のばらつきが大きくなる恐れ
参考にした論文ではナノスケールの微細粉末が強化材でした。
これに対してFRPの強化材である強化繊維は、
数μm以上の繊維が束になっているようなミクロの視点から見ると巨大な構造物が存在します。
陽電子の寿命挙動は強化繊維の影響を受けることは確実であるというのが私見であり、
評価指標にしたい空孔体積も変動する可能性が高いと感じます。
調査によると実際にこのような評価は行われているようですが、
私自身は信頼ある情報には出会っていません。
今後、これに該当するような取り組みがあるようでしたら改めてご紹介したいと思います。
最後に
FRPを含む複合材料はその形態が極めて複雑で不規則のため、
様々な評価軸が必要であると私は考えています。
非破壊検査はその軸を担う重要なもののひとつで、
定番の超音波はもちろん、昨今の高速化と高精度化が進むX線CT、
そしてレーザー励起や超音波加振と赤外線サーモグラフィーを組み合わせた複合非破壊検査、
さらにはX線計測による層間方向に対する応力測定もあります。
トレンドはここに機械学習を入れることですが、
それよりも原理原則をきちんと押さえ、
ブラックボックスなく、安定した非破壊検査ができることこそが本質です。
※参考情報
非破破壊検査を考えるにあたっては今回ご紹介したような陽電子消滅法をはじめ、
通常はナノスケールの薄膜検査を想定している異業種技術に対しても、
線引きすることなく興味を持ち、適用可否の可能性含めて検証を進めるという柔軟さと積極性が重要だと思います。
