FRPの静的材料データの ばらつき 考慮に向けた統計的考え方
今日の はじめてのFRP コラムでは、金属材料を扱われてきた方が最初につまづくであろう、FRPの静的材料データの ばらつき 考慮に向けた統計学の考え方についてご紹介したいと思います。
FRP静的材料データ取得の現実
様々な顧問先企業でも必ず話題になるのが、
「FRPの静的材料データをどう扱うのか」
ということです。
よく見られるケースとして、何となく試験を行い、もう少し高い物性が必要だ、といった議論です。
上記のような要求物性に関する要求や議論ができる、ということは裏を返すと、
最終製品に対する材料の要求事項が十分定量的に精査されている
という前提が必須となっています。
しかし多くの場合、要求事項が「何となく」示されるだけ、または機密なので、ということで開示しないケースが多々見られます。
後者の機密の場合は何らかのやりようがありますが、そもそも要求数値に妥当性が無い場合は、
無駄な材料開発費用と試験費用を消費してしまうことになりかねません。
つまり
静的材料データを取得する目的を明確化する
ということが、実際の試験を進めるにあたり重要になります。
開発が効率的に進むケースが多いのはこのような目的がはっきりしている、
またははっきりさせるために開発の「早い段階」から専門家と協力体制を構築する、
という傾向があるのは間違いなさそうです。
専門的な第三者視点はある程度早い段階から導入することで、より効率的に機能します。
FRP設計開発における静的材料データ取得の目的
静的材料データを取得する目的というのは大きく分けて3つです。
1. CAEに導入するデータ取得
2. SN線図や疲労限度曲線の回帰モデルに用いる
3. 材料規格(材料スペック、Material Spec)に記載する、品質最低要件物性を決める
静的材料データの取得の意義として、上記3点をすぐに述べられる方はそのままデータの取得を進めて問題ありません。
(もしかすると上記3点以外の観点をお持ちかもしれませんが、それは懸念ではありません)
しかし、上記をすべて分かったうえでデータを取られている方にほとんどお会いしたことがない、
というのが現実です。
これは企業の規模の大小、業界違い、国の違いに関わらず見られる傾向です。
上記の3点の詳細はコンサルティングレベルの話なのに加え、
量としても膨大なのでここで詳細は述べられませんが、
大きな方向性として最低でも上記3点を網羅していないとデータ取得の意義が大きく薄れる、
ということはご理解いただいた方がいいと思います。
当然ながらデータを取得されている方がその意義と意味をきちんと理解された上でデータの取得を進めているのであれば、それはとても有意義な開発工程を進められていると考えられます。
FRP材料データに不可避なばらつき
FRPは強化繊維と高分子である樹脂を組み合わせて作る複合材料です。
両者は物理的に分離できる異物同士であるためばらつきは金属や樹脂単体と比較し大きくなる傾向があります。
これらのばらつきを低減させるのに大きな役割を果たすのが材料規格(材料スペック、Material Spec)であり、私のコンサルティングでサポートを行う川下企業のほぼ100%がこの書類が構築できておらず、
かつその必要性があり、私が急遽作成するという状況です。
これによりばらつきを低減させることはできますが、
材料が異物を組み合わせた複合材料である以上、
完全に抑え込むことは不可能である
ことは理解しなくてはいけません。
どちらかというと
このばらつきがどのくらいなのかということを理解した上で使う
ということがFRP設計開発では重要な考え方です。
そしてこのばらつきを把握する際に活用できるツールが統計学です。
FRP静的材料データに活用される統計学
恐らく多くの方が用いられる考え方は正規分布ではないでしょうか。
標準偏差( Standard deviation )は正規分布を前提とした考え方であることはご理解の通りです。
正規分布とは何か、ということを考えた時には以下のような度数分布表が頭に浮かべば正解です。
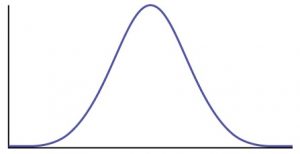
もう少し説明が欲しいということであれば以下のページがとてもわかりやすいです。
http://data-science.gr.jp/theory/tpd_normal_distribution.html
正規分布がガウス分布とも呼ばれる連続確率分布であり、下式で示されるような確率密度関数で示される、
といったことが書かれています。
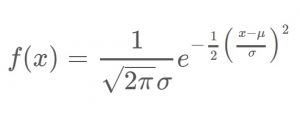
( The image above is referred from http://data-science.gr.jp/theory/tpd_normal_distribution.html )
結論から先に言ってしまうと、多くの場合、この正規分布を基本とした設計思想で進めるケースが多く、
それによる大きな弊害はなさそうである、というのが現段階の私の考え方です。
ただ正規分布ではない考え方も当然あり、その代表格がワイブル分布です。
このコラムで少しだけ触れてみたいと思います。
ワイブル分布も基本は正規分布と同様に連続確率分布ですが、事象の発生確率が一定の場合、
その事象(例えば破壊等)が発生するまでの時間を表す確率変数が指数関数である、
というものになります。
指数関数という言葉、懐かしい響きかもしれません。
ワイブル分布も正規分布同様ネイピア数を用いたものです。
ネイピア数について復習したい方は以下のURLをご参照いただくといいかもしれません。
http://oto-suu.seesaa.net/article/291512873.html
大きな数をできるだけシンプルに扱い、
このシンプルに数字を扱うために細かく刻んでいった時に現れたネイピア数の価値というものを感じます。
やはり技術や科学の本質は改めてとてもシンプルであると感じます。
さて、ワイブル分布については以下のURLがとてもわかりやすいです。
http://data-science.gr.jp/theory/tpd_weibull_distribution.html
細かいことはとりあえずおいておいてFRPにとって重要なところだけ抜粋します。
上記のURLを見ていただくとワイブル分布は、
尺度母数 a と形状母数 b というものを用いて下式で示される確率密度関数であると書かれています。
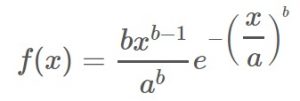
( The image above is referred from http://data-science.gr.jp/theory/tpd_weibull_distribution.html )
T300/5208のCF/Epoxyを用いた過去の研究( L. F. Tenn: ASTM STP, 734, 229, 1981 )によると、
UD材料のT11(0°引張試験)において3母数ワイブル分布への適合性を標本数127という膨大なデータで検証した結果、形状母数が6.76であるという結果が得られているとのことです。
(尚、モデル適合性はコルモゴロフ–スミルノフ検定で行われ、適合性が認められています)
ポイントはここで得られた形状母数の値です。
上述のワイブル分布の説明URLでも述べられていますが、
この形状母数の値はとても重要なデータを提示してくれています。
なぜならば、
尺度母数が一定の場合、形状母数が大きいほど、確率密度関数の形状が正規分布に近づく
ということがわかっているからです。
つまりFRPの静的試験の破壊に関する確率密度関数は正規分布に近い、
ということをワイブル分布でもある程度示すことができているのです。
以下に形状母数(下図中ではcのこと)を変化させたグラフの一例を示します。形状母数が大きいほど正規分布に近い形になっているということがわかると思います。尚、今回話をしている静的材料データではなく、長期寿命評価である動的疲労材料データ等についてはこの形状母数が非常に大きな意味を持っており、形状母数が1より小さいものは初期不具合型、逆に1より大きいものは経年劣化型であると想定できます。何故そう考えるのかについては以下のワイブル分布の確率密度関数の形状を見れば明らかであると思います。
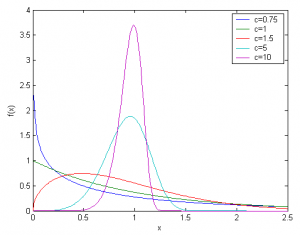
( The image above is referred from http://www.statsref.com/HTML/index.html?weibull.html )
話を元に戻したいと思います。
上記で紹介した以外の過去の文献でも圧縮試験ではその値が8を超えるなど、
軒並みFRPの静的材料試験は形状母数が6を超えており大きなものでは18越えというものもあるようです。
(例: J. M. Whitney, M. Knight, Exper. Mech., 37, 211, 1980 等)
また、ワイブル分布以外についても上記で紹介したL. F. Tennらは、
正規分布、対数正規分布、2母数ワイブル分布についても適合性を検証し、
すべてのモデルに対して適合性が担保できると述べています。
以上のようなことも踏まえ、
FRPの静的試験については正規分布に基づくという仮定をしても大きな問題は無いのではないか、
というのが現段階の私の考えとなっています。
つまりここから先は、破壊確率や確率分布をどのくらいと見積もるのか、
そして危険率をどのくらいにするのか、ということを踏まえ、
正規分布確率表からばらつきの範囲や下限値、上限値を決める、
というのが大まかな流れとなります。
この値設定は設計者ごとに考え方が違うようですので、
そこは設計思想をもって決めていくことが望まれます。
いかがでしたでしょうか。
上記で述べたのはFRP静的材料試験に対する考え方の最初の一歩のあたりを述べたにすぎません。
これらの知見も踏まえ、様々な考え方を盛り込んで設計データを蓄積していく、
という領域からがいわゆる「設計ノウハウ」であるため、
上記で述べたことが参考になるのであれば是非参照いただき、
設計ノウハウを構築していただければと思います。
最後に設計ノウハウの蓄積の仕方のポイントを述べておきます。
1. 必ず明文化しておく(報告書、仕様書など)
2. できる限りシンプルに
この2点はとても重要ですので常に念頭においていただくことをお勧めします。
本コラムがFRP静的材料試験を実施し、データを扱う方々にとって参考になれば幸いです。



